水产养殖常用试验设计方法
出处:按学科分类—农业科学 农业出版社《水产养殖手册》第835页(12233字)
一、试验设计的两个基本步骤
1.处理的构成设计 单因子试验时,一个水平即为一个处理,至少要设两个水平才能进行试验。多因子试验时,每一种水平搭配即为一个试验处理。这种试验处理的构成有两种:一是全面搭配设计,二是正交设计(两两全面搭配设计,详见本节八)这一设计步骤的基本原则是“均衡”。
2.处理的实施设计 对于构成设计的“处理”,根据不同情况,采用不同的实施方法的设计,称为处理的实施设计。通常的设计方法大多就是指这种设计。这一设计的基本原则是要求各试验小区(或试验材料和条件),有同质性。如果小区的排列存在纵、横差异时,可用拉丁方设计,将差异均衡。当横向或纵向之一有差异时,将用随机区组设计方将其均衡。
二、对比试验设计法
1.特点 本法是一种按顺序(或随机)排列的对试验处理的实施设计方法,它可用于单因素试验,也可以用于多因素试验。其特点是:每一供试处理排在对照处理两旁,这样可以使每一个供试处理与相邻对照处理直接比较。
2.设计排列方法
(1)顺序排列法:若以1,2,……n代表供试处理,CK代表对照处理(下同),当有偶数个供试处理时,试验设计排列方式为:

当有奇数个供试处理时,试验设计的排列方法为:

(2)有重复试验的顺向式排列法

(3)有重复试验的逆向式排列法

(4)有重复试验的阶梯式排列法

(5)有重复试验的多排式排列法

3.对比试验设计的优缺点
(1)优点:设计简单,容易掌握。
(2)缺点:对照处理占的较多,会造成人力物力的消耗过大。对三大原则的贯彻不好,且不便于统计分析。
三、间比试验设计法
1.间比试验设计也是处理的实施设计方法,其特点是,在试验处理的排列中,第一个和最后一个一定要安排对照处理CK,每两个对照处理CK之间,要夹相同数目的供试处理。
2.间比试验设计排列法
(1)逆向式排列:

为六个处理二次重复间比试验设计逆向式。
(2)顺向式排列:

为六个处理三次重复间比试验设计顺向式。
3.间比试验设计优缺点
(1)优点:设计简单,容易掌握。
(2)缺点:对照处理占的较多,两对照处理CK间要求夹相同数目的供试处理比较机械,不够灵活。设计中三大原则贯彻得不好,且不便于统计分析。
四、随机区组试验设计法
1.设计方法 随机区组试验设计,是依据局部控制的原则,将试验场地划分为等于重复次数的区组,一个区组即为一个重复,供试的每一个处理在每个区组中仅占有一个且为一个小区,同时每个区组内的小区位置由随机方法排列。当试验场地有明显的条件差异趋势时,区组的划分应与其垂直。
2.安排方式 如图47—4、5。

图47—4 八个处理三次重复随机区组排列示意图
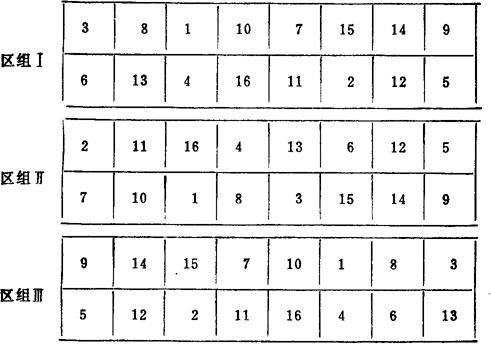
图47—5 十六个处理三个区组随机区组排列示意图
(每个区组中的小区排为两排)
3.随机区组试验设计的优缺点
(1)优点:设计简单、容易掌握、富有弹性、单因素、多因素以及综合试验都可应用。对试验条件要求不严,必要时不同区组可以安排不同地点。能提供无偏的误差估计,便于统计分析。
(2)缺点:处理不宜太多,否则局部控制的效果将会降低。
4.多因素随机区组试验设计举例
(1)在多因素试验中,若采用随机区组设计法,首先需将多因素的各种不同水平进行水平组合,得出试验的处理即完成试验的构成设计,然后把各试验处理随机安排在各个区组,一个区组即为一个重复。
例:欲做A、B、C三因素试验。A分为A1和A2两个水平B分为B1、B2和B3三个水平,C分为C1和C2两个水平。此即为2×3×2型试验,共有水平组合(处理)12个,如表47—2。
表47—2 2×3×2型试验的水平组合表

(2)将以上构成设计的处理按随机区组设计法进行实施设计。若该试验作三次重复(设三个区组),则该试验的试验实施设计方案如下:
当参试因素不是三个,或各因素取其他不同水平时,其设计方法可仿上述进行。

五、拉丁方试验设计法
1.标准拉丁方与非标准拉丁方 凡第一列(左)和第—行(上)按拉丁字母的顺序排列的拉丁方,叫做标准拉丁方。否则,称非标准拉丁方(图47—6)。

图47—6 标准与非标准拉丁方的区别图
2.拉丁方试验设计的特点 拉丁方试验设计是借助于拉丁方表进行的一种处理实施设计。它是将试验处理从行和列两个方向排成区组,而每一试验处理在每一行或每一列都出现且只出现一次。拉丁方试验设计的处理数、重复数、行数和列数均相同。
3.拉丁方试验设计的方法步骤
(1)依据试验处理数目K,从标准拉丁方表中选择一个K×K拉丁方;
(2)随机调动列的顺序;
(3)随机调动行的顺序;
(4)随机决定各拉丁字母代表的处理;
(5)处理与随机完毕的拉丁方表中的拉丁字母“对号入座”,即完成拉丁方试验设计的实施方案。
例:网箱养鱼三种密度试验。三种密度分别用甲、乙、丙表示,采用拉丁方设计的具体步骤是:
①选3×3标准拉丁方(图47—7)

图47—7 3×3标准拉丁方图
②依随机数字顺序2、3、1调动图47—7的列号。即把图47—7中的第二列调到第一列,第三列调到第二列,第一列调到第三列(如图47—8,A)
③再依随机数字顺序1、3、2调动图47—8,A的行号。即第一行不动,第三行调到第二行,第二行调到第三行(如图47—8,B)。
④把处理随机:
乙→A,甲→B,丙→C
⑤“对号入座”。即把处理随机好的甲、乙和丙安排在图47—8,B,即得到拉丁方试验的设计方案(如图47—8,C)。

图47—8 拉丁方设计的调动与“对号”示意图
4.拉丁方设计的优缺点
(1)优点:拉丁方设计,具有从行和列两个方向环境差异的控制,因而试验结果有较高的精度。且利用现成的拉丁方表,设计比较容易掌握。
(2)缺点:拉丁方设计由于要求处理数必须等于重复数,故两者都受到一定的限制,缺乏伸缩性。处理数目不宜太多,否则难于实行局部控制原则。
六、平衡不完全区组试验设计(简称BIB设计)
1.BIB设计的含义 如果试验处理较多,区组容量较小,一个区组只能安排部分试验处理时,就称为不完全区组。在不完全区组设计中,较理想的一种设计法是“平衡不完全区组设计”简称BIB设计。
例:供试处理有1、2、3、4四个,每区组只能安排两个处理(两个小区),则作BIB设计的小区排列方法如图47—9。

图47—9 BIB设计的小区排列图
即共设6个区组,每个处理重复3次,每两个处理相遇于同一区组1次。
BIB设计中的所谓“平衡”,是指各处理之间是平等的;所谓“不完全”,是指每个区组容纳不下全部供试处理,只能容纳部分供试处理。
2.BIB设计特点 BIB设计具有如下两个特点:
(1)每一个处理在每个区组中最多出现一次,总共在r个区组中出现,即每个处理的重复数都是r。如上例中r=3。
(2)每两个处理出现在同一区组的次数λ相等。如上例中λ=1。
3.构成BIB设计的条件 若把BIB设计中的供试处理数记为a,每个区组的小区数记为K,每个处理的重复数记为r,区组总数记为b,每两个处理出现在同一区组的次数记为λ。则a,K,r,b,λ称为BIB设计参数。如上例中的各参数为:
a=4,K=2,r=3,b=6,λ=1。不同的参数就构成不同的BIB设计方案。而这些参数必须满足以下三个条件:
(1)ar=bK

(3)b≥a
4.BIB设计方法步骤
(1)依据试验条件的要求,首先确定BIB参数a,K,r,b,λ的值;
(2)由上述参数查BIB设计表(附表)作出试验方案。
例:网箱养鱼密度试验,设五种不同的放养密度分别用代号1、2、3、4、5表示.由于场地条件限制,每个区组只能容纳三个不同密度的网箱,欲作成BIB设计,应如何安排试验?解:此地a=5,K=3。查BIB设计表的设计4有;a=5,K=3,r=6,b=10,λ=3。其对应的BIB设计表如下:

因此,必须设10个不完全区组,每个区组安排3个不同密度的网箱,每一个密度重复6次,任两个不同密度的网箱,遇于同一区组3次。每区组的具体密度如下(横行为区组)
区组1:1,2,3, 区组2:2,3,4,
区组3:3,4,5, 区组4:4,5,1,
区组5:5,1,2, 区组6:1,2,4,
区组7:2,3,5, 区组8:3,4,1,
区组9:4,5,2, 区组10:5,1,3,
在实际安排时,各区组要随机,各区组内的处理也要随机。本例的BIB设计的具体试验安排如下:

5.BIB设计的优缺点
(1)优点:BIB设计的最大优点在于可使区组不完全,因而当每区组实际可能安排的处理数少于供试处理数时,仍可作出各处理的正确比较。当试验场地比较复杂的情况下,BIB设计是解决矛盾的有效方法。
(2)缺点:BIB设计的缺点是区组数必须按BIB设计表中规定数目设立,缺一不可,否则各处理间的比较就失去均衡性。因而BIB设计的总小区数就相当多,试验规模付出的代价一般较大。
七、多因素的裂区设计法
1.裂区设计的含义 裂区设计是先按第一个因素的水平设置各个处理(主处理)的小区,然后在各主处理的小区内引进第二个因素的各个水平(副因素的),这就是主因素的小区内分设与副因素水平相等的更小的小区。按主因素各水平所分的小区称为“主区”;主区内的副因素各水平所分的小区称为“裂区”。从副因素来讲,主区就是一个区组;但从试验的所有水平组合(处理)讲,主区又是一个不完全区组。由于这种设计将主区分裂为副区,故称为裂区设计。
2.需要采用裂区设计的情况
(1)一个因素各种水平,比另一因素的各种水平可能需要更大的面积时,为了实施和管理上的方便,而应用裂区设计。
(2)试验中某一因素的主效比另一因素的主效更重要时,则把重要因素放在裂区,另一因素放在主区。
(3)当已知某因素的效应比另一因素的效应更大时,可采用裂区设计,把表现较大差异的因素放在主区。
3.裂区设计排列法 若有一项非鲫品种与饵料双因素试验。品种有甲、乙、丙三种;饵料有1,2,3,4四类,且为重要因素。三次重复,其裂区设计排列如下:

图47—10 非鲫品种、饵料二因素试验裂区设计
(品种为主区,饵料为裂区,且都随机安排)
八、多因素的正交试验设计法
1.正交试验的意义和作用 多因素试验的随机区组设计和裂区设计,都是水平组合(或处理)全面实施的试验设计。而水产养殖试验牵扯的因素水平一般都比较多,全面实施都很困难。例如,五因素每因素都有四水平的试验,全面的水平组合共有45=1024个,这些处理全面实施就很困难。如果采用正交表L16(45)进行正交试验,只要16次即可,而且这16次试验从理论和实践上都证明它能达到(或基本上达到)1024次试验的目的。
利用正交表安排的多因素试验设计,称正交试验设计。它是从多因素试验的全部水平组合中,挑出一部分因素水平搭配均匀的有代表性的水平组合来试验的,是一种部分实施的试验。它是目前处理多因素试验的较好设计方法。
2.正交表的含义和种类
(1)正交表Ln(tk)的含义:
其中:L是正交表的代号。
t是参试因素的水平数。
K是正交表的列数,即最多能安排的试验因素的个数。
n是利用这张正交表共需做试验的次数。
例如:表47—3 L9(34)正交表
表47—3 L9(34)正交表

(2)正交表的种类:
①相同水平正交表:如L4(23),L8(27),L9(34)、L16(45),……………(附表3)。
②混合型正交表:即水平不相同的正交表。如L8(4×24),L12(3×24),L16(42×29)……(附表3)。L12(3×24)的含义是:利用这张正交表,可以安排一个三水平的因素,四个二水平的因素,总共需要做12次试验。其他混合型正交表含义类似。
3.正交试验设计的程序
(1)挑因素、选水平:依据试验目的和条件、挑选试验因素,一般以不超过四个为好。各因子取几个水平亦要从实际出发,一般以2—4个水平为宜。
(2)作表头设计:即根据要考查的因素和水平,从附表中选一张“合适”的正交表。选表的原则是:表的水平数一定与试验因素的水平数一致;表的列数不能少于试验因素(包括交互作用)的个数。将试验因素及交互作用确定在正交表列上的工作称为表头设计。
(3)根据设计的表头,把正交表中各列的数字换成该列上因素的水平,便完成了正交试验设计方案。它既包含了“处理”的构成设计,又包含了“处理”的实施设计。
例:关于稚参培育试验。
①确定的因素水平,如表47—4。
表47—4 稚参培育试验设计

②表头设计:此为4因素三水平试验,若不考虑交互作用,可选用正交表L9(34),其表头设计为:

③依表头设计得出利用L9(34)正交表列出的试验设计方案如表47—5:
表47—5 L9(34)正交表列出的试验设计方案表
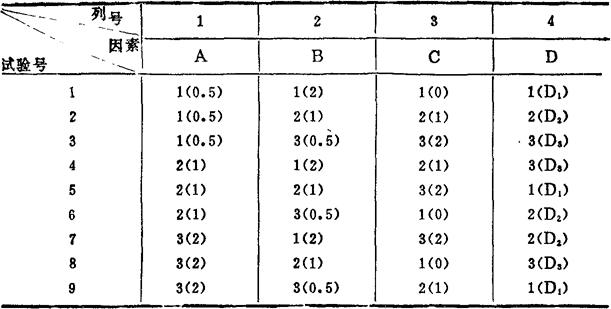
表中括号内数字为相应因素的水平,如第二号试验的因素水平搭配为:幼体密度采用0.5个/m1,投饵量1万个细胞/m1,施呋喃西林1ppm,使用D2方法处理的海水。其他试验号的解释以此类推。
4.水平数不等的正交试验设计法
(1)采用混合型正交表 例如海带养殖五因素不同水平试验:
此为五因素中有一因素(B)为四水平,四个因素为二水平的水平数不等的试验。若不考虑交互作用,可选用混合型正交表L8(4×24)进行正交试验安排,其表头设计如表47—7。即L8(4×24)中第一列安排四水平的B因素,其余各列安排二水平的各因素,表中的数字与水平“对号入座”,即成设计方案。
表47—6 海带养殖试验确定的因素水平表

表47—7 应用混合型正交表L8(4×24)的表头设计

(2)拟水平法:即对水平数不等的正交试验,通过“拟定”水平,化为水平数相等的正交试验。例如:成鱼养殖试验,设计的因素水平如表47—8。
表47—8 成鱼养殖试验的因素水平表

此为不同水平的试验,其中C、D因素为二水平,A、B因素为三水平。若将C的第二水平Ⅱ号饵料重复安排(拟定)一次,把D的第一水平10kg也重复安排(拟定)一次,则变为表47—9的因素水平。
表47—9 成鱼养殖试验的拟定因素水平表

即变为四因素三水平的试验,若不考虑交互作用,可采用正交表L9(34)安排试验即可。
5.有交互作用的正交试验设计
(1)有交互作用的正交试验与没有交互作用的正交试验的主要区别就在于表头设计中要把交互作用当一个“因素”安排,且交互作用这个因素的安排不是任意的,它要受到正交表的交互作用列的约束。下面以L8(27)的交互列表为例,说明如表47—10。
表47—10 L8(27)两列间的交互列表

由上表可查出正交表L8(27)任意两列的交互列。如第一、二列的交互列,可由对角线上的(1)向右横看,同时在对角线上的(2)向上竖看,交叉处的数字“3”即为第一、二列的交互列名(第三列为第一、二列的交互列)。同法可查到第二、四列的交互列为第六列,第三、七列的交互列为第四列等。
(2)有交互作用正交试验设计步骤一般是:
①挑因素定水平。
②确定有交互作用的因素。
③查正交表和它的交互列表作表头设计,安排中应尽量避免因素和交互作用间的混杂。
④写出试验设计方案。
例,有一成鱼养殖试验,其确定的因素水平如表47—11。
表47—11 某成鱼养殖试验因素水平表*

* 设已知A与B,A与C有交互作用。这是一个四因素二水平的试验,因为知A与B、C有交互作用,故查L8(27)及其交互列表(见上)得表头设计为:

6.正交试验选表的参考
表47—12 正交试验设计选表参考表

(编者:孙尽善 审者:刘长安)
附表47—1 标准拉丁方表


附表47—2—1 平衡不完全区组设计(BIB设计)
(阿拉伯数字表示处理,行表示区组,罗马数字表示重复)


附表47—2—2


附表47—2—3

附表47—2—4

附表47—2—5


附表47—2—6


附表47—3—1 常用正交表
(1)水平相同的正交表L4(23)

注 任二列的交互作用为第三列。
L8(27)

附表47—3—2
L6(27)二列间的交互作用列



注 任二列的交互作用为另外二列。
附表47—3—3
L10(215)

附表47—3—4
L16(215)二列间的交互作用列

附表47—3—5

附表47—3—8
L27(313)二列间交互作用列

附表47—3—7 

注 任二列的交互作用为另外三列。
附表47—3—8
L25(56)

注 任二列之交互作用为另外四列。
附表47—3—9
(2)混合型正交表L3(4×24)
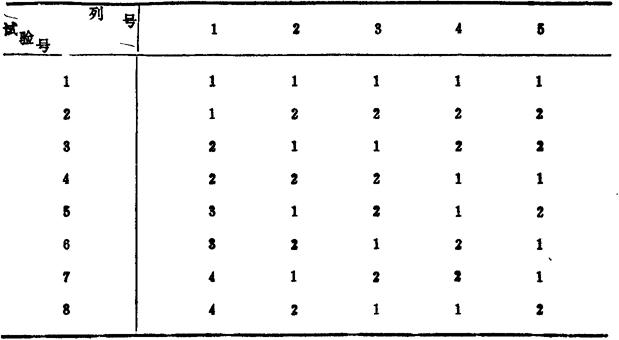
L12(3×24)

附表47—3—10
L16(4×212)

附表47—3—11
L16( )
)

附表47—3—12
L16(43×26)

附表47—3—13
L16(44×22)

附表47—3—14
L16(8×28)

附表47—3—15
L18(2×37)

附表47—3—16
L13(6×34)
