事件的独立性
书籍:数学手册(大学生用)
出处:按学科分类—数理科学和化学 清华大学出版社《数学手册(大学生用)》第373页(1130字)
两事件的独立性 若P(B|A)=P(B),则称B对A是独立的,又叫做A与B独立.
(1)事件A与B独立的充分必要条件是P(AB)=P(A)P(B).
(2)设两事件A,B,0<P(A)<1,A与B独立的充分必要条件是

(3)若事件A与B独立,则A与 ,
, 与B,
与B, 与
与 都相互独立.
都相互独立.
推论 对事件A与B,A与 ,
,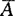 与B,
与B, 与
与 ,只要有一对相互独立,其余三对都相互独立.
,只要有一对相互独立,其余三对都相互独立.
(4)在P(A)>0,P(B)>0的情况下,A与B独立和A与B互斥不能同时成立,即独立一定不互斥,互斥一定不独立.
三事件的独立性
定义1 设A,B,C是三事件,如果

则称三事件A,B,C两两独立.
定义2 设A,B,C是三事件,如果

则称A,B,C为相互独立的事件.
一般地,当事件A,B,C两两独立时,等式
P(ABC)=P(A)P(B)P(C)
不一定成立.
A,B,C两两独立是A,B,C相互独立的必要条件但不是充分条件.
n个事件的独立性 设A1,A2,…,An是n个事件,如果对于任意k(1<k≤n),1≤i1<i2<…<ik≤n,具有等式
P(Ai1Ai2…Aik)=P(Ai1)P(Ai2)…P(Aik),
则称A1,A2,…,An为相互独立的事件.
注 在上式中包含的等式总数为

在实际应用中,对于事件的独立性,往往不是根据定义来判断,而是根据实际意义来加以判断的.
如果已知n个事件相互独立,则对其中的任何k(1<k≤n)个事件,交事件的概率等于其中各个事件概率的乘积.
上一篇:重要分布的数学期望与方差
下一篇:数学手册(大学生用)目录